
UFPr Arts Department
Electronic Musicological Review
Vol. 6 / March 2001
EMR Home - Home - Editorial - Articles - Past Issues
CATEGORISING COMPLEX DYNAMIC SOUNDS
James Correa [1], Eduardo Miranda [2], Joe Wright [3]
Chaosynth is a cellular automata-based granular synthesis system whose abilities to produce unusual complex dynamic sounds are virtually limitless. However, due to its newness and flexibility, potential users have found it very hard to explore the system's possibilities, as there is no clear referential framework to hold on to when designing sounds. Standard software synthesis systems take the importance of this framework for granted by adopting a taxonomy for synthesis instruments that has been inherited from the acoustic musical instruments tradition, i.e. woodwind, brass, string, percussion, etc. Sadly, the most interesting synthesised sounds that these systems can produce are simply referred to as effects. This scheme clearly does not do justice to the capabilities of more innovative software synthesisers. In order to alleviate this problem, we propose an alternative taxonomy for Chaosynth timbres. The paper describes the basic functioning of Chaosynth and presents our proposed taxonomy, concluding with remarks on further work currently underway.
1 Granular synthesis and cellular automata
Granular synthesis works by generating a rapid succession of very short sound bursts called granules (e.g. 35 milliseconds long), which together form larger sound events (Gabor 1947; Miranda 1998). The results tend to exhibit a great sense of movement and sound flow. This synthesis technique can be metaphorically compared with the functioning of a motion picture in which an impression of continuous movement is produced by displaying a sequence of slightly different images at a rate above the scanning capability of the eye. So far, most of these systems have used complex mathematical formulae (e.g. probabilities) to control the production of the granules, determining, for example, the waveform and the duration of the individual granules. We devised a system called Chaosynth (Miranda 1995) that uses a different method: cellular automata (Cood 1968).
In general, cellular automata (CA) are implemented as a grid of variables referred to as cells. Each cell may assume values from a finite set of integers and each value is normally associated with a colour. The functioning of a cellular automaton is displayed on the computer screen as a sequence of changing patterns of tiny coloured cells, like an animated film. At each frame, the values of all cells change simultaneously, according to a set of transition rules that takes into account the values of their neighbourhood. The CA used in Chaosynth is called ChaOs, an acronym for Chemical Oscillator. An in-depth understanding of the mathematics behind ChaOs is not necessary to operate Chaosynth. It suffices to know how the algorithm works and its general behaviour: from an initial random distribution of cells in the grid, the automaton tends to drive the cells towards an oscillatory cycle of patterns (Figure 1).

Figure 1: ChaOs tends to evolve from an initial random distribution of cells in the grid towards an oscillatory cycle of patterns.
The behaviour of ChaOs resembles the way in which most of the natural sounds produced by some acoustic instruments evolve: they tend to converge from a wide distribution of their partials (for example, noise) to oscillatory patterns; for example, a sustained tone. ChaOs can be thought of as an array of identical electronic circuits called cells. At a given moment, cells can be in any one of the following conditions: quiescent, depolarised or burned. A cell interacts with its neighbours (4 or 8) through the flow of electric current between them. There are minimum (Vmin) and maximum (Vmax) threshold values which characterise the condition of a cell. If its internal voltage (Vi) is under Vmin, then the cell is quiescent (or polarised). If it is between Vmin (inclusive) and Vmax values, then the cell is being depolarised. Each cell has a potential divider which is aimed at maintaining Vi below Vmin. When the divider fails (that is, if Vi reaches Vmin) the cell becomes depolarised. There is also an electric capacitor which regulates the rate of depolarisation. The tendency, however, is that cells become increasingly depolarised with time. When Vi reaches Vmax, the cell fires and becomes burned. A burned cell at time t is automatically replaced by a new quiescent cell at time t + 1.
2 Rendering sounds from ChaOs
Each sound granule produced by Chaosynth comprises several spectral components. Each component is a waveform produced by a digital oscillator (i.e., a lookup sampling table containing one cycle of a waveform) which needs three parameters to function: frequency, amplitude and duration (in milliseconds) of the signal. ChaOs controls the frequency and duration values of each granule, but the amplitude values are set up by the user beforehand. That is, the spectral contours of the granules are established before hand via Chaosynth’s Oscillators panel (Figure 2), but the actual frequency content of the spectrum is controlled by ChaOs.

Figure 2: A sample screen shot of Chaosynth featuring the Oscillators panel. Each column on the main window controls the amplitude for a table lookup oscillator.
The values (i.e., the colours) of the cells are associated with frequencies (these values are set via Chaosynth’s Frequency panel); and oscillators are associated with a number of cells. The frequencies of the components of a granule at time t are established by the arithmetic mean of the frequencies associated with the values of the cells associated with the respective oscillators. Suppose, for example, that each oscillator is associated with 9 cells and that at a certain time t, 3 cells correspond to 110 Hz, 2 to 220 Hz and the other 4 correspond to 880 Hz. In this case, the mean frequency value for this oscillator at time t will be 476.66 Hz. An example of a grid of 400 cells allocated to 16 oscillators of 25 cells each is shown in Figure 3. The user can also specify the dimension of the grid, the amount of oscillators, the allocation of cells to oscillators, the allocation of frequencies to CA values, and various other CA-related parameters. The duration of a whole sound event is determined by the number of CA iterations and the duration of the particles; for example, 100 iterations of 35 millisecond particles result in a sound event of 3.5 seconds of duration.
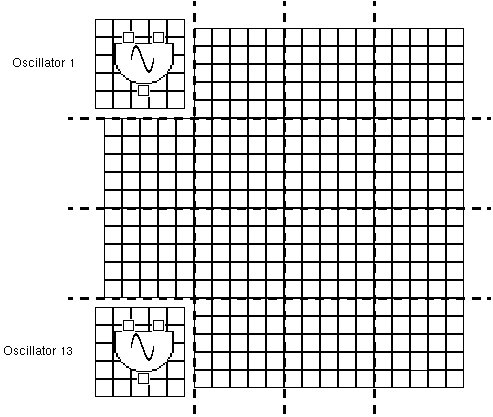
Figure 3: An example of a grid of 400 cells allocated to 16 digital oscillators
3 Chaosynth and sound design
Chaosynthhas proved to be a incredibly powerful synthesiser, whose abilities to produce unusual sounds are virtually limitless. The main criticism that we have received from its potential users, however, is that due to its newness and flexibility, it has been very hard to explore its potential: users other than Chaosynth’s makers themselves do not have a clear reference to begin the sound design process. The problem is that standard software synthesis systems take for granted the role of a taxonomy for synthesis instruments by adopting categories inherited from the acoustic musical instruments tradition: i.e. woodwind, brass, string, percussion, etc. Sadly, the most interesting synthesised sounds that these system can produce are simply referred to as effects. This scheme clearly does not do justice to the capabilities of more innovative software synthesisers. In order to alleviate this problem, we propose an alternative taxonomy for Chaosynth timbres. This new taxonomy is based on a framework for sound categorisation (Figure 4) inspired by Pierre Schaeffer’s (1966) concept of sound maintenance and, to some extent, by an article written by Jean-Claude Risset in the book Le timbre, métaphore pour la composition (1991). We assume that the most important characteristic of the sounds produced by Chaosynth, and granular synthesis in general, is their spectral evolution in time (Miranda 1998). Our proposed taxonomy is introduced below. Note that we will use the term "instrument" to refer to specific Chaosynth setups that produce the sounds of the respective categories.
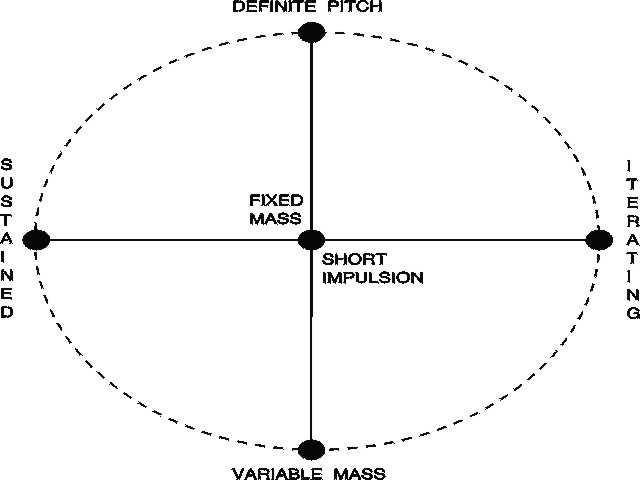
Figure 4: A framework for sound categorisation.
4 The proposed taxonomy
The general structure of the proposed taxonomy is portrayed in Table 1. We have defined five general classes: Fixed Mass, Flow, Chaotic, Explosive and General Textures.
Table 1: The five main classes of our taxonomy and some sub-classes.
| Fixed Mass |
Flow |
Chaotic |
Explosive |
General Textures |
| Lighten |
Cascade |
Insects |
Metallic |
Textures |
| Darken |
Landing |
Melos |
Woody |
Effects |
| Dull |
Raising |
Boiler |
Glassy |
|
| Elastic |
Lift |
Windy |
Blower |
|
| Melted |
Crossing Drift |
Noises |
Drum |
4.1 Fixed Mass
This class comprises those instruments that produce sounds formed by a large amount of small grains. The overall outcome from these instruments is perceived as sustained sounds with a high degree of internal redundancy, that is, fixed mass. Notice here that by fixed mass we do not mean fixed pitch, but rather a stable and steady spectrum where the frequencies of the grains are kept within a fixed band. Sometimes this creates a sense of pitch, but this phenomenon is not a mandatory condition. We have defined five sub-classes for this class: whilst Lighten are bright instruments that produce sounds rich in high frequencies, Darken are those instruments that produce sounds rich in low frequencies; Dull instruments produce muffled sounds, and finally Elastic and Melted were named after the psychoacoustic sensation they create. Figure 5 shows a sonogram of a typical fixed mass sound, or instrument, in our nomenclature (Sound example 1).
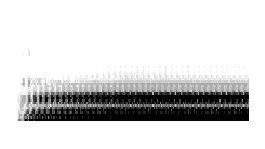
Figure 5: A Fixed Mass sound is perceived as sustained with a high degree of internal redundancy.
4.2 Flow
These are instruments whose outcome gives a clear sensation of movement due to a continuous change of the fundamental frequencies of the grains. These sounds are said to have a variable mass, but not an unpredictable one as the frequencies of the grains tend to move collectively in one direction. Six sub-classes for this class were defined according to the direction of the spectral movement: Cascade and Landing, both comprise instruments whose outcome is of a descending direction, with the difference that the movement of the former is smooth and light, whereas in the latter it is fast and vigorous. Conversely, there are Raising and Lift instruments, where the movement is ascending. The Crossing instruments produce sounds that display a cross movement between two groups of frequencies, one group going upwards and the other going downwards. Finally, the sub-class Drift, produces sounds whose sense of direction is not entirely clear; there is some flow but frequencies of the grains tend to "drift" up or down. Figure 6 portrays the sonogram of a Cascade-type of sound (Sound example 2).

Figure 6: The sonogram of a Flow-type of sound whereby the frequencies of the grains are of a descending nature.
4.3 Chaotic
This class of instruments produces sounds with a very large degree of spectral movement. These sounds are of highly variable mass, the movement of the grain frequencies is unpredictable and they do not have an overall direction. We have defined five sub-classes of chaotic instruments: Insects, are those instruments whose outcome resemble the noises produced by insects. These sounds have more activity in the high frequencies. Melos produce sounds in which the individual grains can be perceived as individual notes as if they were fast melodic fragments (Figure 7), whereas the sounds from a Boiler instrument resemble the sounds of boiling liquids. Windy and Noises produce sounds that resemble or are derived from white-noise: the former produces an auditory sensation of blowing air, whereas the latter produces noise similar to an AM radio off station (Sound example 3).

Figure 7: The sonogram of a Melos sound.
4.4 Explosive
This class resembles traditional acoustic percussion instruments. The sounds here are of short duration, fast attack, practically no sustain and short decay; in general terms, these sounds have a short impulsion and are either of a fixed or variable mass (Figure 8). This class comprises five sub-classes, organised according to the resemblance of their sounds to those from real percussive materials: Metallic, Woody, Glassy, Blower and Drum. Blower instruments produce explosion-like sounds with a fast and very high energy. In the Drum class we include those instruments whose sounds are very similar to membrane-type drums (Sound example 4).

Figure 8: The sonogram of an Explosive Metallic timbre.
4.5 General Textures
These are instruments that produce what we refer to as musical gestures. They are divided into two sub-classes: Textures and Effects. The outcome of Textures is clouds of sounds with long duration and a variable mass. The classic example here is the typical bubbly and cloudy-like stereotype texture that is normally associated with granular synthesis. The second sub-class, the Effects, generates sounds that resemble some standard musical instrument techniques, such as a cello glissando, or metaphorical sounds such as the noise of a steam train, a helicopter or a Klingon phaser (Sound example 5).
5 Conclusion
The development of the proposed taxonomy is the result of massive experimentation with Chaosynth. There are still some inconsistencies to be addressed. We feel, for example, that the General Textures class is still too vague in comparison with the others. We are currently devising a large catalogue of instruments classified according to this taxonomy to distribute to Chaosynth users. Our aim is to gather as much feedback as possible from the users in order to implement further improvements.
References:
COOD, E.F., Cellular Automata, London (UK): Academic Press, 1968.
GABOR, D., Acoustical Quanta and the Theory of Hearing, Nature, Nr. 1044, pp. 591-594, 1947.
MIRANDA, E. R., Chaosynth: Um sistema que utiliza um automato celular para sintetizar partículas sônicas. II SBC&M Proceedings, Porto Alegre: Instituto de Informatica da UFRGS, 1995.
MIRANDA, E. R., Computer Sound Synthesis for the Electronic Musician. Oxford (UK): Focal Press, 1998.
RISSET, J.-C., Timbre et synthèse des sons. In Le timbre: métaphore pour la composition, J.-B. Barrière (Ed.), IRCAM: Christian Bourgois Editeur, 1991.
SCHAEFFER, P., Traité des objets musicaux, Paris: Editions du Seuil, 1966.
(1) Laboratório de Música
Eletroacústica de Santa Maria, Orquestra Sinfônica da UFSM, Santa
Maria - RS, Brazil. jcorrea1@ix.netcom.com
(2) SONY Computer Science Laboratory Paris, 6 rue Amyot,
75005 Paris, France. miranda@csl.sony.fr
(3) Nýr Sound, 8 Cringle Av., Bournemouth, Dorset BH6
4HX, United Kingdom. joe@nyrsound.com
Chaosynth is available for both Windows and Macintosh computers. For more information please refer to the Nyr Sound web site.
Other sound examples are available at http://emr.topcities.com/Miranda/ (copy and paste it in the address bar).